How Do Computers 'Decide'? A Fun Guide to Finite Automata

TOC Simplified: A Beginner's Guide to the 'Grammar' of Computers

TOC stands for Theory of Computation. The name sounds a bit scary, but you can think of it as the "grammar" of computer science. Just like English grammar has rules for making sentences, TOC has rules for what kind of problems a computer can solve and how efficiently it can solve them. It’s a very important subject in GATE because it builds the foundation for everything else you study.

The Building Blocks - Symbols, Alphabets, and Strings.

Before we build a machine, we need to know what it reads. In TOC, machines read strings, which are made of:

• Symbols: These are just the basic characters. For example, a, b, c are symbols, and so are 0 and 1.
• Alphabets (Σ): An alphabet is simply a collection of symbols. For example, a binary alphabet is Σ = {0, 1}.
• Strings: A string is a sequence of symbols from an alphabet. For example, using the binary alphabet, "0110", "101", and "000" are all valid strings.

Now that we know about strings, let's talk about the machine that reads them. The simplest machine in TOC is called a Finite Automata (FA).Think of it like a ticket barrier at a metro station. It only has a few states (like 'gate open' or 'gate closed') and it changes its state based on an input (like you inserting a valid token). A Finite Automata works just like that. Its only job is to read a string of symbols and decide if that string is "Accepted" or "Rejected".There are two main types of FA:

1. DFA (Deterministic Finite Automata)
2. NFA (Non-deterministic Finite Automata)

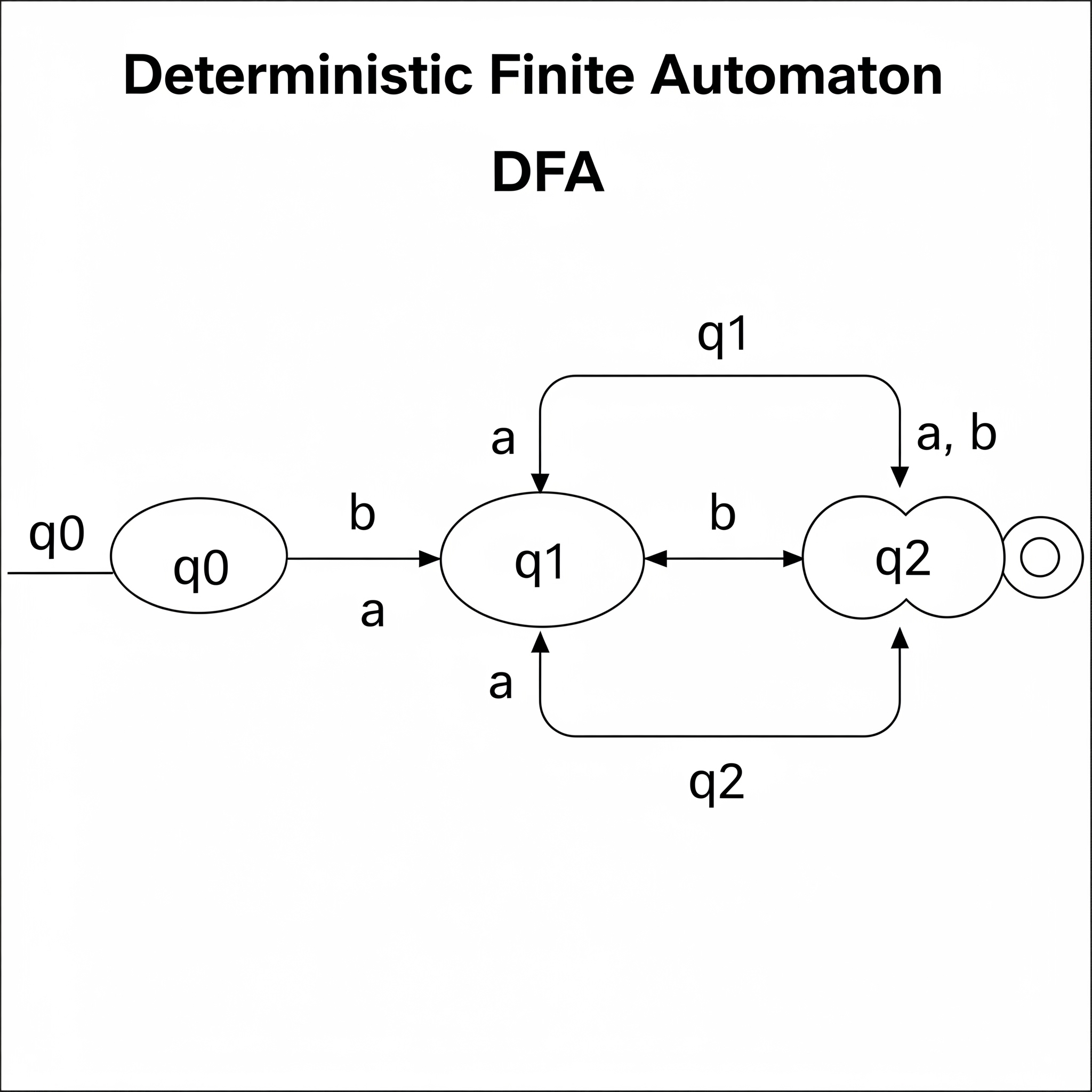
The 'D' in DFA stands for Deterministic. This means the machine is very strict and predictable. For any state and any input symbol, there is only ONE single path to the next state. There is no confusion or choice. It's like a robot that has a fixed, pre-decided instruction for every possible situation.

 NFA (Non-deterministic Finite Automata) - The Flexible Machine

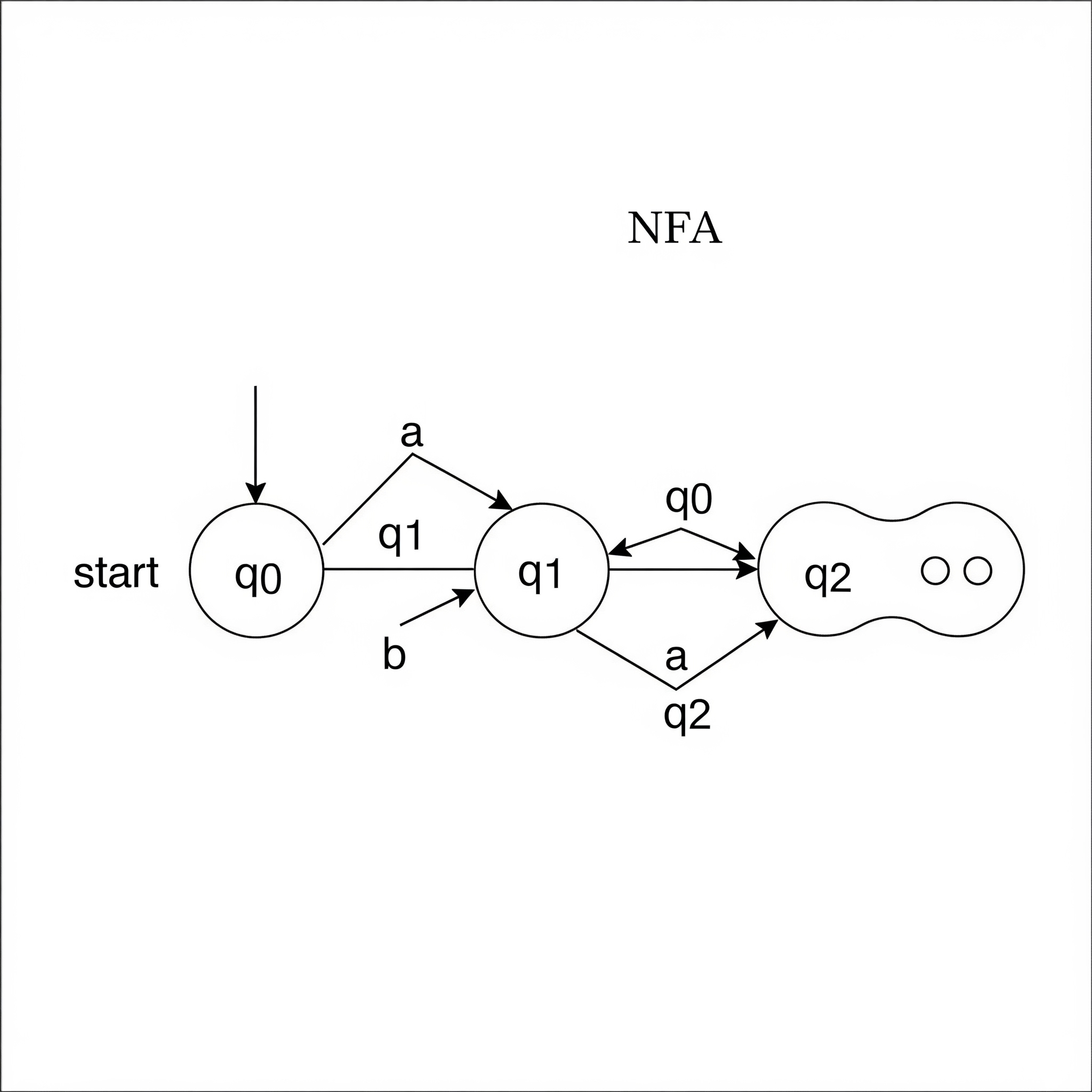
The 'N' in NFA stands for Non-deterministic. This machine is more flexible. For a state and an input symbol, it can have multiple possible next states. It's like having 'choices'. This flexibility often makes it much easier to design an NFA for a given problem compared to designing a DFA for it.

These concepts can be tricky, but a visual explanation can make all the difference. To see these machines in action, watch our complete 'TOC Basics' masterclass on YouTube! 

Watch the full video here: TOC ALL Basics - Complete Lecture by GO Classes

Conclusion: Your First Step to Mastery

So, let's quickly recap. We've learned that TOC is the 'grammar' of computers and covered its basic building blocks like alphabets and strings. We also explored the simplest machines, Finite Automata, and understood the difference between the 'strict' DFA and the 'flexible' NFA.Congratulations! By understanding these core concepts, you've built a powerful foundation for mastering the Theory of Computation. This is the first and most important step on your journey. 

Ready to dive deeper and master every topic in Theory of Computation? Explore the complete GO Classes course for GATE and build the confidence to solve any problem.

Enroll in the GO Classes GATE Course Now